尝试在博客中添加简易文章推荐功能

把文档转换成 “向量”，并且尝试用线性代数等数学工具来解决信息检索这类问题，至少可以追溯到 20 世纪 70 年代。想到在 Hexo 这种静态博客系统，特别是 GitHub Page 这种 Serverless 服务中使用 Word2Vec 等深度学习方法似乎并不现实，所以这里使用的是一个非常简单经典的 TF-IDF 算法.

TF-IDF 算法原来是搜索引擎中的核心部分，谷歌百度已经使用 TF-IDF 作为内容排名因素很长一段时间.

现在的搜索引擎一般用如下的算法计算网站页面得分：score (页面得分) = TFIDF 分 * x + 链接分 * y + 用户体验分 * z（其中 x+y+z=100%），TFIDF 分值百度大约占 40% 左右的权重，谷歌更是达到了 50%.

这是百度的计算方法： score (页面得分) = 40% 的内容质量相关性（TFIDF）+ 40% 的用户体验分 + 20% 的链接分（域名 + 外链）.

搜索引擎使用 TF-IDF 来计算内容质量相关性，我们这边也可以用它来计算文章内容相关性，然后实现简易文章推荐功能。

当然也可以使用文章的 tags 标签最为推荐依据，但是这样过于依赖人工标注数据，顺便最近发现在 Hexo 中分类和标签只能在 source/_posts 文件夹中使用才能渲染出来。

构建向量空间模型

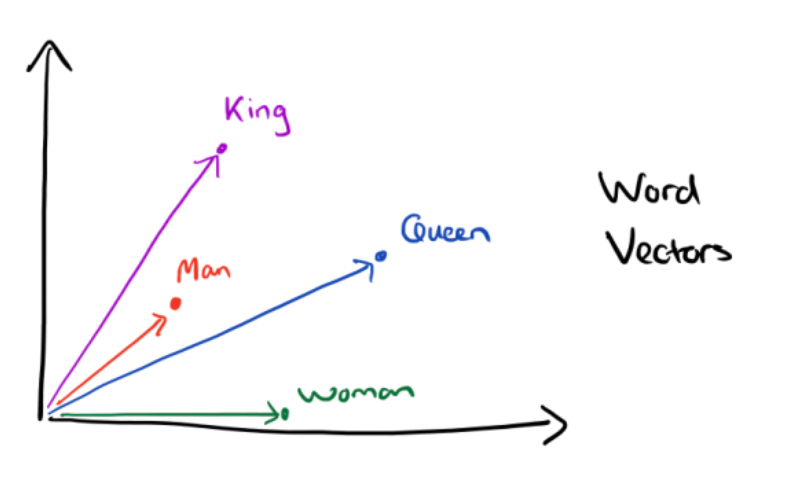
将文档转化为向量来表示，这样文档与文档之间就可以定量的去度量他们之间的关系，挖掘文档之间的联系。上面提到的 Word2Vec 是把单词转化为向量来表示，这样词与词之间就可以定量的去度量他们之间的关系，挖掘词之间的联系.

比如将词的维度降维到 2 维，用下图的词向量表示词:

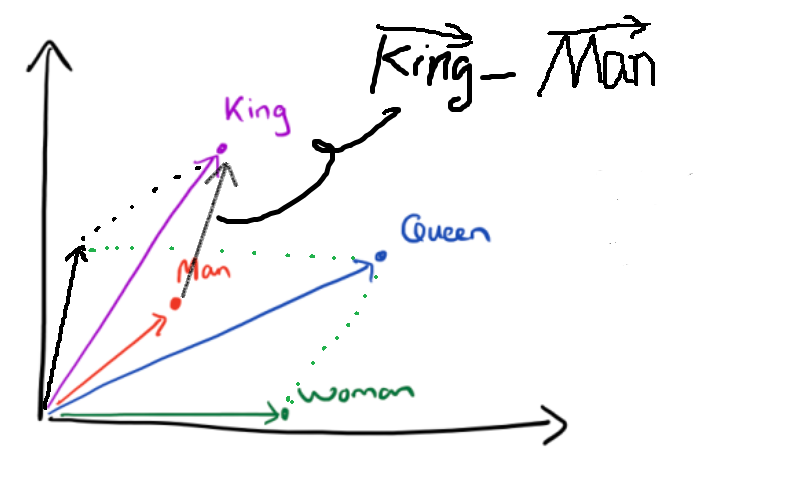
似乎发现了什么不得了的事情。

对于自然语言书写的文本这种非结构化信息，从文本中抽取出的特征来量化来表示文本信息，构建向量空间模型，并基于数学模型的处理，将文本转换为机器可以理解的语言的方式是很重要的。

举个栗子

要实现文章推荐，就需要从一堆文章中找出一些内容相似的文章。基本思路就是，如果文章的关键词越相似，那么他们的内容就会越相似。

我们先从几个简单的句子着手。

句子A：我这里有苹果和西瓜。

句子B：我喜欢吃西瓜，不喜欢吃苹果。

句子C：我喜欢吃蔬菜。

第一步：数据清洗

简单去除标点符号等干扰信息。

句子A: 我这里有苹果和西瓜

句子B: 我喜欢吃西瓜 不喜欢吃苹果

句子C: 我喜欢吃蔬菜

第二步：分词

使用分词工具进行分词。

句子A:

[ '我', '这里', '有', '苹果', '和', '西瓜' ]

句子B:
[
  '我', '喜欢',
  '吃', '西瓜',
  '不', '喜欢',
  '吃', '苹果'
]

句子C:

[ '我', '喜欢', '吃', '蔬菜' ]

第三步：去重收集所有句子中所有的词

[
  '我',   '这里', '有',
  '苹果', '和',   '西瓜',
  '喜欢', '吃',   '不',
  '蔬菜'
]

第四步：计算词频

词频背后的假设是文章的重要程度即文章的相关度与单词在文档中出现的次数成正比。文章的关键词应当比文章中的其他词出现的次数多。

$词频某个词在文章中出现的次数$

句子A:

{
  '我': 1,
  '这里': 1,
  '有': 1,
  '苹果': 1,
  '和': 1,
  '西瓜': 1,
  '喜欢': 0,
  '吃': 0,
  '不': 0,
  '蔬菜': 0
}

句子B:
{
  '我': 1,
  '这里': 0,
  '有': 0,
  '苹果': 1,
  '和': 0,
  '西瓜': 1,
  '喜欢': 2,
  '吃': 2,
  '不': 1,
  '蔬菜': 0
}

句子C:

{
  '我': 1,
  '这里': 0,
  '有': 0,
  '苹果': 0,
  '和': 0,
  '西瓜': 0,
  '喜欢': 1,
  '吃': 1,
  '不': 0,
  '蔬菜': 1
}

第四步：词频标准化

文章的篇幅有长有短，为了便于不同文章的比较，进行” 词频” 标准化。词频标准化的目的是把所有的词频在同一维度上分析。

词频标准化有两种方案：

方案一：

$词频某个词在文章中出现的次数文章的总词数$

方案二：

$词频某个词在文章中出现的次数该文出现最多的词出现的次数$

一般情况下，第二个标准化方案更适用，因为能够使词频的值相对大点，便于分析。

有时候常常用这个值来代替原来的 TF 取值。这样的计算保持了一个平衡，既有区分度，但也不至于完全线性增长。

这里使用比较简单的方案一作为栗子：

句子A:

{
  '我': 0.16666666666666666,
  '这里': 0.16666666666666666,
  '有': 0.16666666666666666,
  '苹果': 0.16666666666666666,
  '和': 0.16666666666666666,
  '西瓜': 0.16666666666666666,
  '喜欢': 0,
  '吃': 0,
  '不': 0,
  '蔬菜': 0
}

句子B:
{
  '我': 0.125,
  '这里': 0,
  '有': 0,
  '苹果': 0.125,
  '和': 0,
  '西瓜': 0.125,
  '喜欢': 0.25,
  '吃': 0.25,
  '不': 0.125,
  '蔬菜': 0
}

句子C:

{
  '我': 0.25,
  '这里': 0,
  '有': 0,
  '苹果': 0,
  '和': 0,
  '西瓜': 0,
  '喜欢': 0.25,
  '吃': 0.25,
  '不': 0,
  '蔬菜': 0.25
}

第五步：计算逆文档频率

仅有词频 (TF) 不能比较完整地描述文档的相关度。因为语言的因素，有一些单词可能会比较自然地在很多文档中反复出现，比如这里中的 “我”、“和” 等等。这些词大多起到了链接语句的作用，是保持语言连贯不可或缺的部分。

很明显，如果有太多文档都涵盖了某个单词，这个单词也就越不重要，或者说是这个单词就越没有信息量。因此，我们需要对词频 (TF) 的值进行修正，而逆文档频率 (IDF) 的想法是用文档频率 (DF) 的倒数来进行修正。

$逆文档频率语料库的文档总数包含该词的文档数$

如果一个词越常见，那么分母就越大，逆文档频率就越小越接近 0。分母之所以要加 1，是为了避免分母为 0（即所有文档都不包含该词）。log 表示对得到的值取对数。为什么要用 log 函数？log 函数是单调递增，求 log 是为了归一化，保证逆文档频率不会过大。用 Log 进行变换，也是一个非线性增长的技巧，这样的计算保持了一个平衡，既有区分度，但也不至于完全线性增长。

句子A:

{
  '我': -0.2876820724517809,
  '这里': 0.4054651081081644,
  '有': 0.4054651081081644,
  '苹果': 0,
  '和': 0.4054651081081644,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0.4054651081081644,
  '蔬菜': 0.4054651081081644
}

句子B:
{
  '我': -0.2876820724517809,
  '这里': 0.4054651081081644,
  '有': 0.4054651081081644,
  '苹果': 0,
  '和': 0.4054651081081644,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0.4054651081081644,
  '蔬菜': 0.4054651081081644
}

句子C:

{
  '我': -0.2876820724517809,
  '这里': 0.4054651081081644,
  '有': 0.4054651081081644,
  '苹果': 0,
  '和': 0.4054651081081644,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0.4054651081081644,
  '蔬菜': 0.4054651081081644
}

第六步：计算 TF-IDF

$词频逆文档频率$

可以看到，TF-IDF 与一个词在文档中的出现次数成正比，与该词在整个文档库中的出现次数成反比。

句子A:

{
  '我': -0.047947012075296815,
  '这里': 0.06757751801802739,
  '有': 0.06757751801802739,
  '苹果': 0,
  '和': 0.06757751801802739,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0,
  '蔬菜': 0
}

句子B:
{
  '我': -0.03596025905647261,
  '这里': 0,
  '有': 0,
  '苹果': 0,
  '和': 0,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0.05068313851352055,
  '蔬菜': 0
}

句子C:

{
  '我': -0.07192051811294523,
  '这里': 0,
  '有': 0,
  '苹果': 0,
  '和': 0,
  '西瓜': 0,
  '喜欢': 0,
  '吃': 0,
  '不': 0,
  '蔬菜': 0.1013662770270411
}

第七步：列出文档向量

这里准确来说应该是 TF-IDF 特征向量，这是一个稀疏矩阵。下面把它作为描述文章特征的向量。

说明一点，这里的文章的特征不是由某几个关键词的 TF-IDF 值决定的，而是由所有的词的 TF-IDF 值共同决定的。

句子A:

[
  -0.047947012075296815,
  0.06757751801802739,
  0.06757751801802739,
  0,
  0.06757751801802739,
  0,
  0,
  0,
  0,
  0
]

句子B:

[
  -0.03596025905647261,
  0,
  0,
  0,
  0,
  0,
  0,
  0,
  0.05068313851352055,
  0
]

句子C:

[
  -0.07192051811294523,
  0,
  0,
  0,
  0,
  0,
  0,
  0,
  0,
  0.1013662770270411
]

可以对文档向量进行标准化，使得这些向量能够不受向量里有效元素多少的影响，也就是不同的文档可能有不同的长度。把向量都标准化为一个单位向量的长度。这个时候再进行点积运算，就相当于在原来的向量上进行余弦相似度的运算。

第八步：计算余弦相似度

到这里，如何寻找两篇相似文章的问题转变成了如何计算这两个向量的相似程度的问题。

什么叫做向量相似？

一般地，如果两个向量平行或重合，我们认为这两个向量相似度为。如果这两个向量垂直，或者说正交，我们认为这两个向量的相似度为。

以二维空间为例，和是两个向量，我们要计算它们的夹角。余弦定理告诉我们，可以用下面的公式求得：

假定和是两个维向量，我们把这些向量放到维欧几里得空间中讨论，向量之间的距离使用欧几里得距离。

假定是，是，则与的夹角的余弦等于：

{
  '句子A': {
    '句子A': 1.0000000000000002,
    '句子B': 0.21934876427664535,
    '句子C': 0.21934876427664535
  },
  '句子B': {
    '句子A': 0.21934876427664535,
    '句子B': 1,
    '句子C': 0.33484380220099325
  },
  '句子C': {
    '句子A': 0.21934876427664535,
    '句子B': 0.33484380220099325,
    '句子C': 1
  }
}

第九步：余弦相似度按照降序排序

两两计算向量夹角的余弦值，然后按降序排列，取排在最前面的几个文章，就是相似度较高的文章，作为推荐结果。

{
  '句子A': {
    '句子A': 1.0000000000000002,
    '句子B': 0.21934876427664535,
    '句子C': 0.21934876427664535
  },
  '句子B': {
    '句子B': 1,
    '句子C': 0.33484380220099325,
    '句子A': 0.21934876427664535
  },
  '句子C': {
    '句子C': 1,
    '句子B': 0.33484380220099325,
    '句子A': 0.21934876427664535,
  }
}

相同句子的余弦值是 . 余弦值越接近，就表明夹角越接近度，也就是两个向量越相似.

第十步：收集推荐结果

{
  '句子A': [ '句子B', '句子C' ],
  '句子B': [ '句子C', '句子A' ],
  '句子C': [ '句子B', '句子A' ]
}

即：

A-B
B-C
C-B

A 和 C 之间没什么关系。

源码实现

Volantis 主题实现文章推荐

https://github.com/volantis-x/hexo-theme-volantis/blob/684c40333b16b5d1df1a9e4a7f1da90216e5a17a/scripts/helpers/ 文章推荐.js

~~UI 界面是随手写的，又不是不能用（~~

代码变量是中文写的，方便易读。其实是中间出 Bug 了，然后调试 Debug 时顺便整的活

本文采用 GLWT（Good Luck With That，祝你好运）公共许可证许可协议，转载请注明出处。